números reales

  números reales 

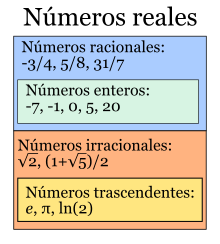
Un número real puede ser un número racional o un número irracional. Los números racionales son aquellos que pueden expresarse como el cociente de
 dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demás. ... El conjunto de los números racionales se designa mediante .

espero te puedas guiar con este vídeo ☺

TALLER 1: CONOCIENDO LOS NÚMEROS REALES Y SUS PROPIEDADES GRADOS-11

  

PRE-PRUEBA

 1) Si A={1,2,3,4,5,6}, B={2,4,6} y C={1,3,5,7} determine si los siguientes enunciados 

      son ciertos o falsos:

      

     a) 1∈ B 

     b) B⊂ A

2) Para los conjuntos A={1,2,4,5,7}, B={2,4,9} y C={4,9} realice las siguientes 

    operaciones: 

    a) A∪B 

    b) A∩C

        

3) Determine si los siguientes números son racionales o irracionales: 

   a) .3422123123123... 

   b) .10110111001111... 

   b)  11/9

4) Indique cuáles axiomas de los números reales se usaron para realizar las siguientes operaciones: 

 a) 3+(2+1)=(3+2)+1 

 b) 2(3+4)=(3+4)2 

5) Simplifique usando el orden de las operaciones.

  a) [2+(2-3)](-2) 

  b) 3[2+(-3-4)]

6) Determine cuál de los axiomas de orden se usa para justificar los 

siguientes enunciados:

   

  a) Si 2<3, entonces 4<5. 

  b) Si 2<3, entonces 8<12 

7) Determine si los siguientes números son primos o compuestos:

 a) 31

 b) 91 

 8) Encuentre el divisor común mayor de los siguientes pares de números:

 a) 2 y 4

 b) 6 y 27

9) Determine si los siguientes enunciados son ciertos o falsos:

a) 2 ∈ B 

 b) C ⊆ B

 c) 3 ∈ C 

 d) A ⊂ C 

 e) 1 ∈ ∅ 

 f) 3 ∉ B 

 g) C ⊆ / A 

10) Determine si las siguientes expresiones son ciertas o falsas:

 a) 1 ∈ Q

 b) -1 ∈ N

 c) N ∩ I=∅

 d) Z ⊂ Q

 e) Q ∪ I=R

 f) Q ∩ I=R

número entero 

Un número entero es un elemento del conjunto numérico que contiene los números naturales ${\displaystyle \mathbb {N} =\{1,2,3,4,\cdots \}}$, sus opuestos y el cero.¹​ Los enteros negativos, como −1 o −3 (se leen «menos uno», «menos tres», etc.), son menores que cero y todos los enteros positivos  Para resaltar la diferencia entre positivos y negativos, se puede escribir un signo «más» delante de los positivos: +1, +5, etc. Y si no se escribe signo al número se asume que es positivo.

El conjunto de todos los números enteros se representa por la letra ${\displaystyle \mathbb {Z} =\{...,-3,-2,-1,0,+1,+2,+3,\,...\}}$ 

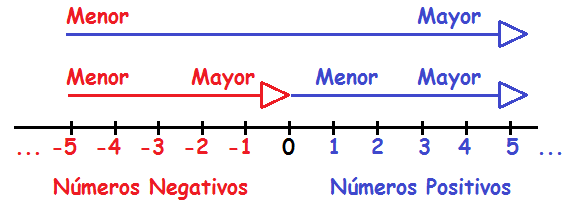
En la recta numérica los números negativos se encuentran a la izquierda del cero y los positivos a su derecha.

Los números enteros pueden sumarse, restarse , multiplicarse  y dividirse , siguiendo el modelo de los números naturales añadiendo unas normas para el uso del signo

spero te pueda servir este vídeo

espero te pueda servir este vídeo☺

TEMA. NÚMEROS ENTEROS  EJERCICIOS GRADO 11 

1. • 1. En una estación de esquí la temperatura más alta ha sido de -2⁰ C, y la más baja, de -23⁰ C. ¿Cuál ha sido la diferencia de temperatura

   
   

• 2. Un avión vuela a 11000 m y un submarino está a -850 m. ¿Cuál es la diferencia de altura entre ambos?

• 3. En la cuenta corriente del banco tenemos 1250 €. Se paga el recibo de la luz, que vale 83 €; el recibo del teléfono, que vale 37 €, y dos cheques de gasolina de 40 € cada uno. ¿Cuánto dinero queda en la cuenta corriente?

 Cristina vive en el 4º piso, se sube en el ascensor y baja al sótano 2, ¿Cuántos pisos ha bajado?

• 9. Tengo en el banco 60 €, me ha llegado una factura de 100 €, ¿cuánto me falta para pagar la factura?

•  Si estoy en el piso 2º y bajo 3 pisos ¿en cual me sitúo?

números irracionales 

En matemáticas , un número irracional es un número que no puede ser expresado como una fracción ^m⁄_n, donde m y n sean enteros y n sea diferente de cero.​ Es cualquier numero real que no es racional , y su expresión decimal no es ni exacta ni periódica.

Un decimal infinito (es decir, con infinitas cifras) periódico, como √7 = 2,645751311064591... no puede representar un número racional. A tales números se les nombra "números irracionales". Esta denominación significa la imposibilidad de representar dicho número como razón de dos números enteros. El numero pi (${\displaystyle \pi }$), numero e y el numero euro (${\displaystyle \phi }$) son otros ejemplos de números irracionales.

espero te sirva el siguiente vídeo ☻

DESCARGAR PRUEBA https://drive.google.com/file/d/1saPjeaCyI4hq8G4SgtxnJZE2ifWqhsgg/view?usp=sharing 

NÚMEROS TRASCENDENTES 

PARTE FINAL 

Un número trascendente (o trascendental) es un tipo de numeroirracion que no es raíz de ningún polinomio (nonulo) con coeficientes enteros (o racionales). En este sentido, número trascendente es antónimo de numeroalgebraico  La definición no proviene de una simple relación algebraica, sino que se define como una propiedad fundamental de las matemáticas.

Tipo de número irracional que no proviene de una simple relación algebraica sino que se define como una propiedad fundamental de las matemáticas. Un número es trascendente (o trascendental) si no es raíz de ningún polinomio (no nulo)

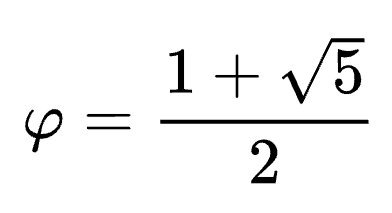
descarga la prueba https://drive.google.com/file/d/1cgedHIu8cAHKUKUmbpZgAww2SIzquuxj/view?usp=sharing